VGGNet
VGGNet
- Very Deep Convolutional Networks for Large-Scale Image Recognition
- Karen Simonyan∗ & Andrew Zisserman+
- https://arxiv.org/pdf/1409.1556.pdf
简介
VGGNet由牛津大学的视觉几何组(Visual Geometry Group)和 Google DeepMind公司的研究员一起研发的的深度卷积神经网络,在 ILSVRC 2014 上取得了第二名的成绩,将 Top-5错误率降到7.3%。
VGGNet论文给出了一个非常振奋人心的结论:卷积神经网络的深度增加和小卷积核的使用对网络的最终分类识别效果有很大的作用。
网络结构
结构
- 输入到卷积网络的是一个修复过的大小为224*224的RGB图像(图像预处理是将每个像素减去在训练集上计算的平均RGB值),处理后迭代更少,更快收敛,加速网络训练。
- 卷积层所用的卷积核为3×3大小(这是能抓住上下左右以及中间所有信息的最小的卷积核大小);有些卷积层中还使用了1×1大小的卷积核(FC层之间的),可看作是输入通道的线性变换。卷积步幅固定为1像素,3×3卷积层的填充设置为1个像素。
- 池化层采用空间池化,空间池化有五个最大池化层,他们跟在一些卷积层之后,但是也不是所有的卷积层后都跟最大池化。最大池化层使用2×2像素的窗,步幅为2。
- 卷积层后跟三个FC层:第一、二个FC层有4096个通道,第三个FC层执行1000路ILSVRC分类因此包括1000个通道(通道对应每个类别)。
- 所有网络的全连接层配置相同。最后一层是softmax层,用来分类。
- 所有隐藏层都有ReLU非线性函数,网络除了第一个其他都不包含局部响应归一化(LRN)
配置
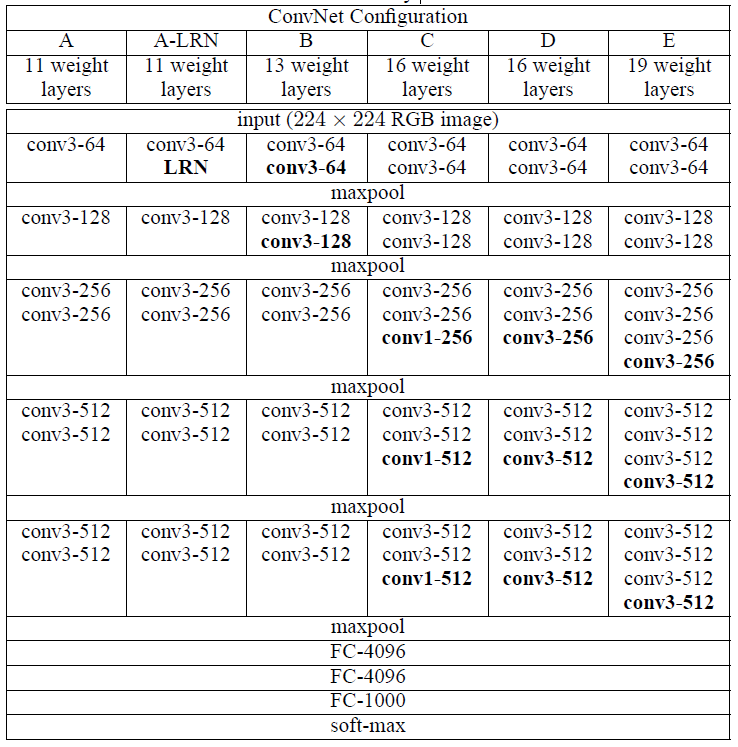
- 从左(A)到右(E),随着层数的增加,卷积层参数表示为conv<感受野尺寸>-<通道数量>
- 所有卷积网络层的配置都是参照AlexNet原则做的
- 注:层数只计算卷积层和全连接层
参数量如下表:

VGG16
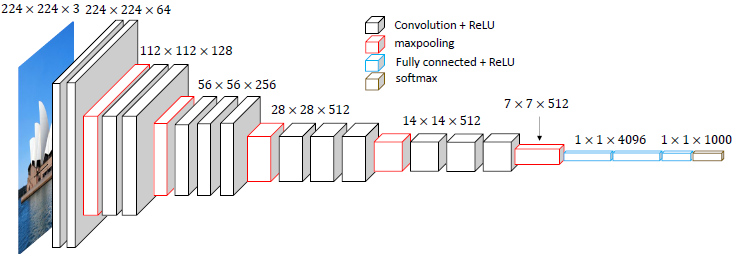
现在最常用的VGG网络为VGG16,就是D列所示结构,图示如下:
细节理解
细节1
相比于其他网络,VGG 网络的一个改进点是将 大尺寸的卷积核用多个小尺寸的卷积核代替。比如:VGG使用 2个3X3的卷积核 来代替 5X5的卷积核,3个3X3的卷积核 代替7X7的卷积核。
好处:
-
在保证相同感受野的情况下,多个小卷积层堆积可以提升网络深度,增加特征提取能力(非线性层增加)。
感受野相同的原因:假设图片大小是28×28,使用5×5的卷积核对其卷积,步长为1,卷积后得到的结果是:(28-5)/1+1=24;
然后使用2个卷积核为3×3的,这里的两个是指2层:
第一层3*3:卷积后得到的结果是(28-3)/1+1=26
第二层3*3:卷积后得到的结果是(26-3)/1+1=24
所以我们的最终结果和5*5的卷积核是一样的。
-
参数更少。
5*5卷积核:5×5+1=26
两个3*3卷积核:3×3+1+3×3+1=20
cnn感受视野
在卷积神经网络中,决定某一层输出结果中一个元素所对应的输入层的区域大小,被称为感受野(receptive field)。
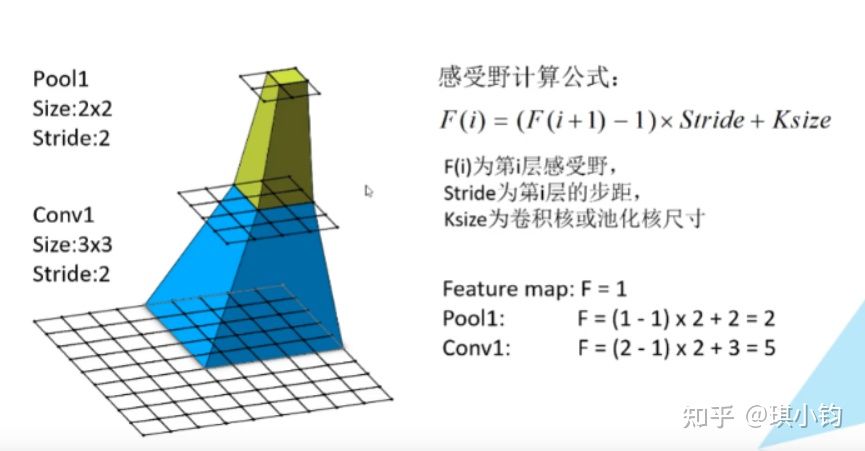
感受野公式
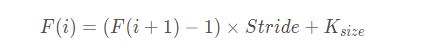
细节2
在FC层中间采用dropout层,防止过拟合,如下图:
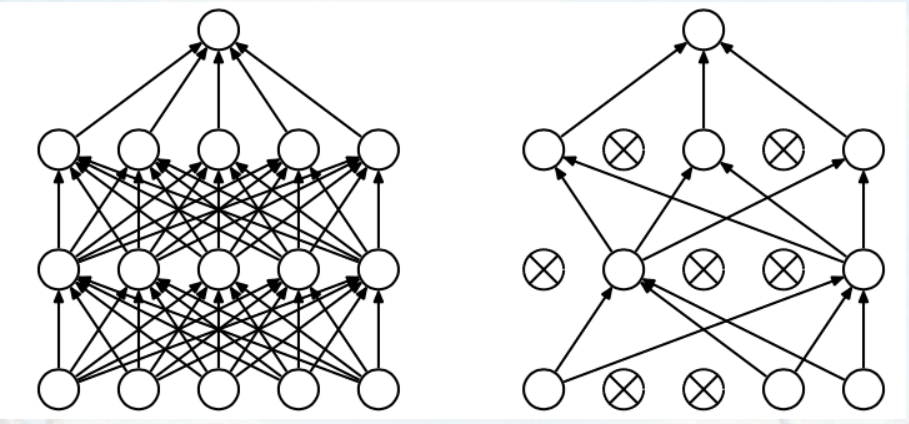
上图左边的为一个完全的全连接层,右边为应用 dropout 后的全连接层。
我们知道,典型的神经网络其训练流程是将输入通过网络进行正向传导,然后将误差进行反向传播。dropout 就是针对这一过程之中,随机地删除隐藏层的部分单元,进行上述过程。步骤为:
(1)、随机删除网络中的一些隐藏神经元,保持输入输出神经元不变;
(2)、将输入通过修改后的网络进行前向传播,然后将误差通过修改后的网络进行反向传播;
(3)、对于另外一批的训练样本,重复上述操作 (1)。
原理为:
(1)、达到了一种投票的作用。对于单个神经网络而言,将其进行分批,即使不同的训练集可能会产生不同程度的过拟合,但是我们如果将其公用一个损失函数,相当于对其同时进行了优化,取了平均,因此可以较为有效地防止过拟合的发生。
(2)、减少神经元之间复杂的共适应性。当隐藏层神经元被随机删除之后,使得全连接网络具有了一定的稀疏化,从而有效地减轻了不同特征的协同效应。也就是说,有些特征可能会依赖于固定关系的隐含节点的共同作用,而通过 dropout 的话,就有效地组织了某些特征在其他特征存在下才有效果的情况,增加了神经网络的鲁棒性。
分类框架
训练
-
卷积网络训练步骤大致跟随AlexNet,除了从多尺度训练图像中对输入进行采样,也就是说通过使用小批量梯度下降法优化多项式逻辑回归来进行训练。批量大小为:256,动量为:0.9。训练通过权重衰减(L2惩罚函数设置为5*10^-4)和Dropout正则化对前两层FC层作用(Dropout率设置为0.5)。学习率初始化设置为:0.01,然后当验证集准确率停止增加时学习率衰减为原来的0.1,总之学习率要减小三次,在370K次迭代(74epoch之后)停止学习。
-
初始化权重:网络配置A随机初始化,然后对更深层次网络结构,将前四层卷积层和后三个FC层都按照A网络的初始化配置设置,中间层接着随机初始化。没有减少预初始化层的学习率,而是让它们随着学习的进程发生改变。
对于随机初始化,我们从一个均值为0方差为0.01的正态分布中对权重进行采样,偏置初始化为0
发现:使用随机初始化程序可以在不进行预训练的情况下初始化权重。
-
从重缩放的训练集图像中进行随机裁剪(每次SGD迭代每幅图像都要做一次裁剪)。为进一步增加训练集,输入图像需要做随机水平翻转和随机RGB颜色偏移。
训练图像重缩放:两种固定尺度的模型(①S=256,应用于AlexNet,ZFNet,Sermanet;②S=384)。
考虑两种设定训练规模S的方法:
方法一:给定一个卷积网络配置,首先使用S=256训练网络,为了加速S=384网络的训练,它使用S=256预训练的权重进行初始化,使用初始学习率为0.003。
方法二:多尺度训练,每个训练图像通过从某个范围中随机采样S来单独重缩放(范围为[256,512])
测试
将全连接层等效替换为卷积层进行测试
原因是:卷积层和全连接层的唯一区别就是卷积层的神经元和输入是局部联系的,并且同一个通道(channel)内的不同神经元共享权值(weight)。卷积层和全连接层的计算实际上相同,因此可以将全连接层转换为卷积层,只要将卷积核大小设置为输入空间大小即可:例如输入为7x7x512,第一层全连接层输出4096;我们可以将其看作卷积核大小为7x7,步长为1,没有填充,输出为1x1x4096的卷积层。这样的好处在于输入图像的大小不再受限制,因此可以高效地对图像作滑动窗式预测;而且全连接层的计算量比较大,等效卷积层的计算量减小了,这样既达到了目的又十分高效。
为什么卷积层可以“代替”全连接层?
卷积和全连接的区别大致在于:卷积是局部连接,计算局部信息;全连接是全局连接,计算全局信息。(但二者都是采用的点积运算)
但如果卷积核的kernel_size和输入feature maps的size一样,那么相当于该卷积核计算了全部feature maps的信息,则相当于是一个kernel_size∗1的全连接。在全连接层上,相当于是n∗m(其中n是输入的维度,m是输出的维度)的全连接,其计算是通过一次导入到内存中计算完成;如果是在最后一个feature maps上展开后进行的全连接,这里若不进行展开,直接使用output_size的卷积核代替,则相当于是n∗1的全连接(这里的n就是feature maps展开的向量大小,也就是卷积核的大小kernel_size∗kernel_size),使用m个卷积核则可以相当于n∗m的全连接层。
但用卷积层代替全连接层的方式,其卷积核的计算是并行的,不需要同时读入内存中,所以使用卷积层的方式代替全连接层可以加开模型的优化。
结果
1 单尺度
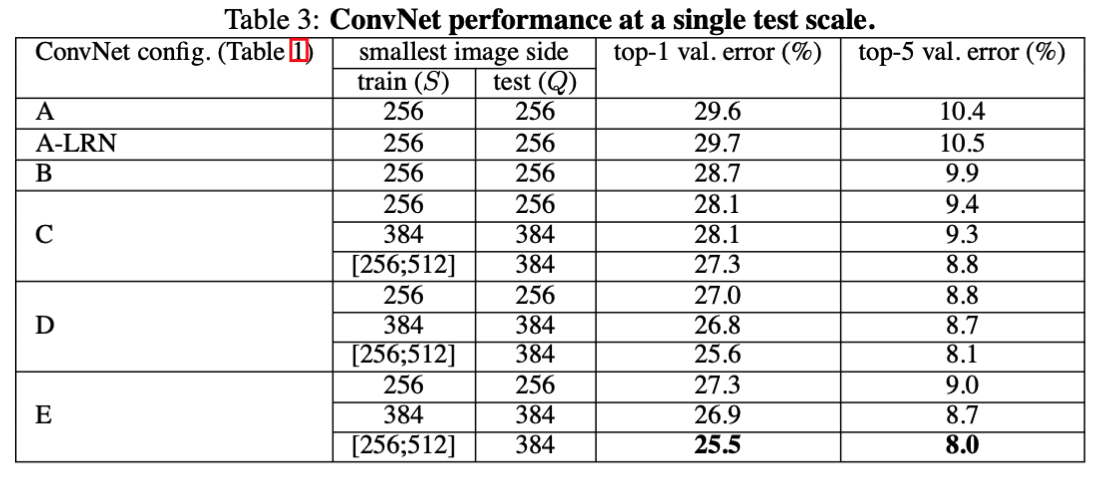
- 模型E(VGG19)的效果最好,即网络越深,效果越好
- 同一种模型,随机scale jittering的效果好于固定S大小的256,384两种尺度,即scale jittering数据增强能更准确的提取图像多尺度信息
2 多尺度
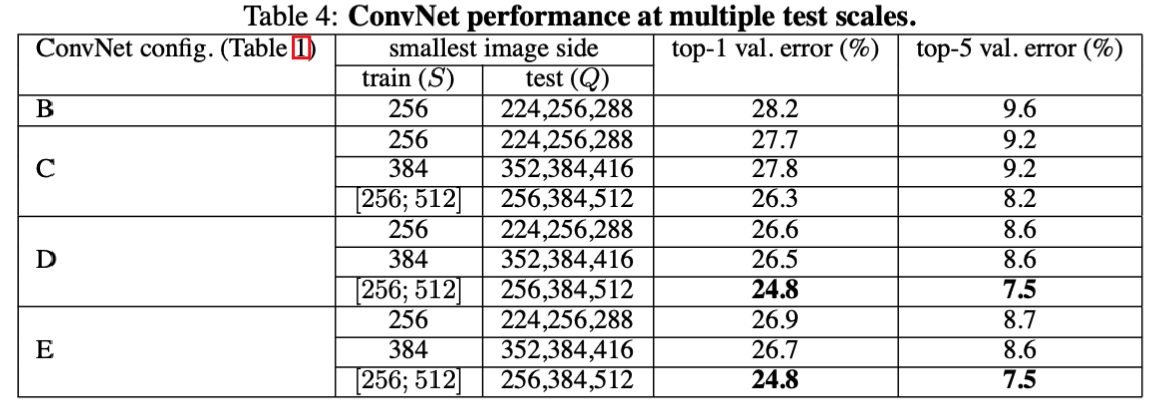
- 对比单尺度预测,多尺度综合预测,能够提升预测的精度
- 同单尺度预测,多尺度预测也证明了scale jittering的作用
3 多尺度裁剪
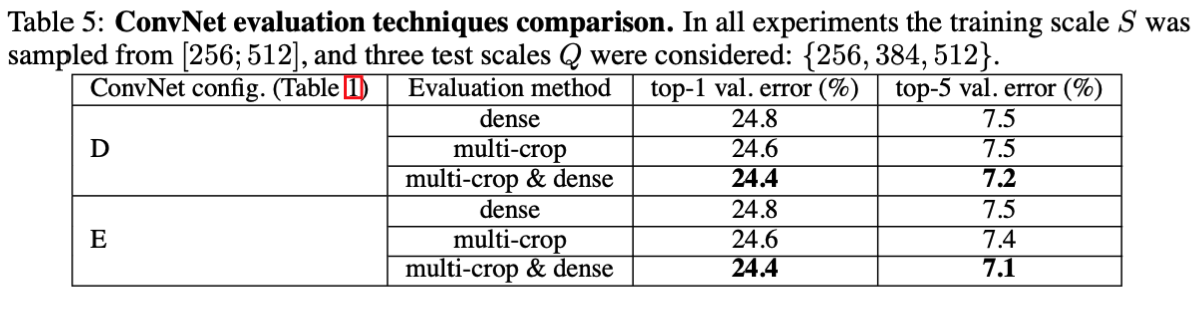
- 数据生成方式multi-crop效果略优于dense,但作者上文也提到,精度的提高不足以弥补计算上的损失
- multi-crop于dense方法结合的效果最好
- 最后,也证明了作者的猜想:multi-crop和dense两种方法互为补充
4 模型融合

- 通过多种模型融合输出最终的预测结果,能达到最优的效果
5 对比
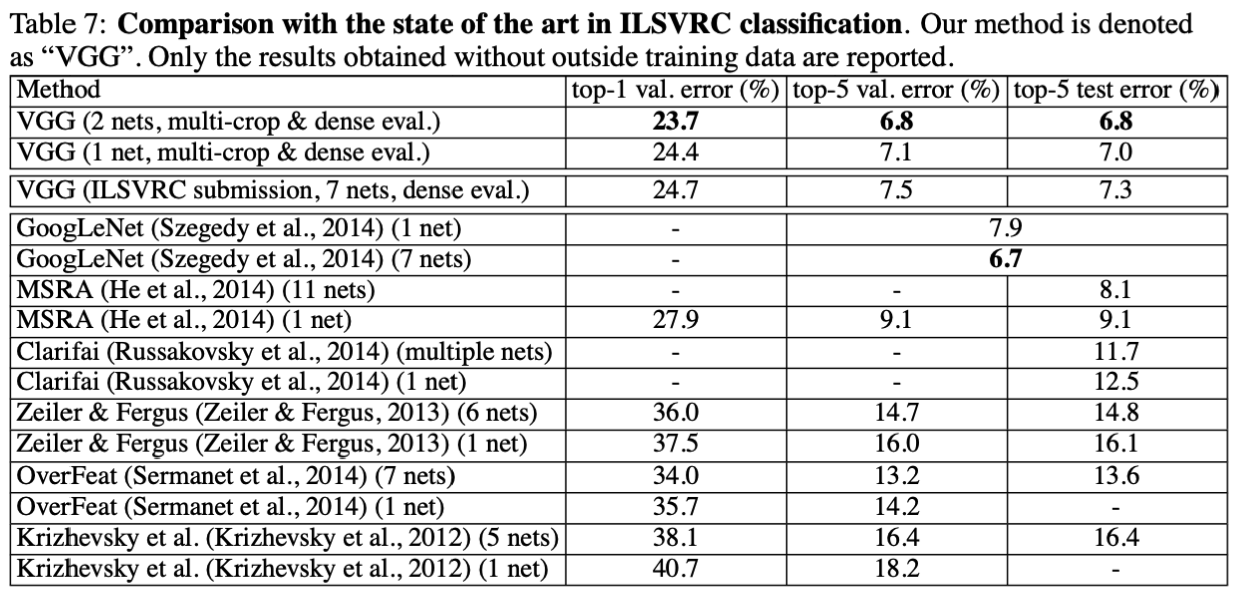
- 与其他模型对比发现,VGG也能达到非常好的效果。
总结
深度对网络正确率的影响是有益的,但是总得来说该网络还是比较臃肿。
论文中采用的技巧:
- 卷积块叠加在一起,即加深网络深度。2卷+池化+2卷+池化+3卷+池化+3卷+池化+3卷+池化+3FC,从左向右尺寸越来越小,通道数越来越大。
- 使用小卷积核:增加了非线性性、减少参数量且感受野大小相同。大部分使用3×3卷积核,有些卷积层使用1×1。两个3×3=一个5×5,三个3×3=一个7×7。
- 保留了AlexNet中的ReLU和dropout。
- 测试时将全连接层转换为卷积层,这样就可以输入任意大小的图像了,也就是说测试时用全卷积网络。同时也用到全局平均池化。
- 训练时采用多尺度